刷题汇总（五）leetcode 热题 HOT 100 C++ 答案总结

发表于 | 分类于 ， ， | 阅读次数:

题目来源

leetcode 热题 HOT 100题

相关：
刷题汇总（一）leetcode 精选50题 JavaScript答案总结
刷题汇总（二）剑指Offer 66题 C++答案总结
刷题汇总（三）leetcode 精选50题 C++答案总结
刷题汇总（四）技术类编程题汇总 C++
刷题汇总（六）leetcode 多线程 / Shell

PDF版 code （提取码：0wxr ）

1、两数之和

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。

你可以假设每种输入只会对应一个答案。但是，你不能重复利用这个数组中同样的元素。

示例:

给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    // 时间复杂度：O(n)，空间复杂度：O(n)
    vector<int> twoSum(vector<int>& nums, int target) {
        vector<int> res(2);
        unordered_map<int,int> map;
        for(int i=0;i<nums.size();i++){
            int tmp = target - nums[i];
            if(map.find(tmp)!=map.end()){
                res[0] = i;
                res[1] = map[tmp];
                break;
            }
            map[nums[i]] = i;
        }
        return res;
    }
};

2、两数相加

给出两个 非空 的链表用来表示两个非负的整数。其中，它们各自的位数是按照 逆序 的方式存储的，并且它们的每个节点只能存储 一位 数字。

如果，我们将这两个数相加起来，则会返回一个新的链表来表示它们的和。

您可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例：

输入：(2 -> 4 -> 3) + (5 -> 6 -> 4)
输出：7 -> 0 -> 8
原因：342 + 465 = 807

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
 // 时间复杂度：O(max(m,n))，空间复杂度：O(max(m,n))， 新列表的长度最多为max(m,n)+1
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode* res = new ListNode(0);
        ListNode* head = res;
        int flag = 0;
        while(l1 || l2){
            int x = l1?l1->val:0;
            int y = l2?l2->val:0;
            head->next = new ListNode((x+y+flag)%10);
            flag = x+y+flag>9?1:0;
            if(l1) l1 = l1->next;
            if(l2) l2 = l2->next;
            head = head->next;
        }
        if(flag==1){
            head->next = new ListNode(1);
        }
        return res->next;
    }
};

3、无重复字符的最长子串

给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

输入: “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。
示例 2:

输入: “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”，所以其长度为 1。
示例 3:

输入: “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”，所以其长度为 3。
请注意，你的答案必须是 子串 的长度，”pwke” 是一个子序列，不是子串。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 时间复杂度：O(n)，空间复杂度：O(m)，m 是字符集的大小
class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int res = 0;
        unordered_map<char,int> map;
        int i = 0;
        for(int j=0;j<s.size();j++){
            if(map.find(s[j])!=map.end()){
                i = max(map[s[j]],i);
            }
            map[s[j]] = j+1;
            res = max(j-i+1, res);
        }
        return res;
    }
};

4、寻找两个有序数组的中位数

给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。

请你找出这两个有序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。

你可以假设 nums1 和 nums2 不会同时为空。

示例 1:

nums1 = [1, 3]
nums2 = [2]

则中位数是 2.0
示例 2:

nums1 = [1, 2]
nums2 = [3, 4]

则中位数是 (2 + 3)/2 = 2.5

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    // 时间复杂度：O(log(min(m,n)))，空间复杂度：O(1)O(1)
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        if(nums1.size()>nums2.size())
            return findMedianSortedArrays(nums2,nums1);
        int m = nums1.size(), n = nums2.size();
        int lmax1,rmin1,lmax2,rmin2,c1,c2,low=0,heigh=2*m;
        while(low <= heigh){
            int c1 = (low+heigh)/2;
            int c2 = m+n-c1;
            lmax1 = c1 == 0? INT_MIN:nums1[(c1-1)/2];
            rmin1 = c1 == 2*m? INT_MAX:nums1[c1/2];
            lmax2 = c2 == 0? INT_MIN:nums2[(c2-1)/2];
            rmin2 = c2 == 2*n? INT_MAX:nums2[c2/2];
            if(lmax1>rmin2) heigh = c1-1;
            else if(lmax2>rmin1) low = c1+1;
            else break;
        }
        return (max(lmax1,lmax2)+min(rmin1,rmin2))/2.0;
    }
};

5、最长回文子串

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: “babad”
输出: “bab”
注意: “aba” 也是一个有效答案。
示例 2：

输入: “cbbd”
输出: “bb”

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    // 时间复杂度：O(n^2)，空间复杂度：O(1)
    string longestPalindrome(string s) {
        int start=0, len=0;
        for(int i=0;i<s.size();i++){
            int tmp = max(getsub(i,i,s),getsub(i,i+1,s));
            if(tmp>len){
                len = tmp;
                start = i-(len-1)/2;
            }
        }
        return s.substr(start,len);
    }

    int getsub(int i,int j,string s){
        while(i>=0 && j<s.size() && s[i]==s[j]){
            i--;
            j++;
        }
        return j-i-1;
    }
};

6、正则表达式匹配

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。

‘.’ 匹配任意单个字符
‘*’ 匹配零个或多个前面的那一个元素
所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

说明:

s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母，以及字符 . 和 *。
示例 1:

输入:
s = “aa”
p = “a”
输出: false
解释: “a” 无法匹配 “aa” 整个字符串。
示例 2:

输入:
s = “aa”
p = “a*”
输出: true
解释: 因为 ‘*’ 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 ‘a’。因此，字符串 “aa” 可被视为 ‘a’ 重复了一次。
示例 3:

输入:
s = “ab”
p = “.*”
输出: true
解释: “.*” 表示可匹配零个或多个（’*’）任意字符（’.’）。
示例 4:

输入:
s = “aab”
p = “cab”
输出: true
解释: 因为 ‘*’ 表示零个或多个，这里 ‘c’ 为 0 个, ‘a’ 被重复一次。因此可以匹配字符串 “aab”。
示例 5:

输入:
s = “mississippi”
p = “misisp*.”
输出: false

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    bool isMatch(string s, string p) {
        const char* str = s.c_str();
        const char* pattern = p.c_str();
        return match(str,pattern);
    }

    bool match(const char* str, const char* pattern)
    {
        if(*str == '\0' && *pattern == '\0') return true;
        if(*str != '\0' && *pattern == '\0') return false;
        if(*(pattern+1) != '*'){
            if(*str==*pattern || *pattern=='.'&&*str!='\0'){
                return match(str+1,pattern+1);
            }
            else return false;
        }
        else{
            if(*str==*pattern || *pattern=='.'&&*str!='\0'){
                return match(str,pattern+2)|| match(str+1,pattern+2)|| match(str+1,pattern);
            }
            else return match(str,pattern+2);
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    // 时间复杂度：O(TP)，空间复杂度：O(TP)
    bool isMatch(string s, string p) {
        int l1 = s.size(),l2 = p.size();
        vector<vector<bool>> dp(l1+1,vector<bool>(l2+1));
        dp[l1][l2]=true;
        for(int i=l1;i>=0;i--){
            for(int j=l2-1;j>=0;j--){
                bool tmp = i<l1 && ( s[i] == p[j] || p[j] == '.');
                if(j+1<l2 && p[j+1] == '*'){
                    dp[i][j] = dp[i][j+2] || tmp && dp[i+1][j];
                }
                else{
                    dp[i][j] = tmp && dp[i+1][j+1];
                }
            }
        }
        return dp[0][0];
    }
};

7、盛最多水的容器

给定 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。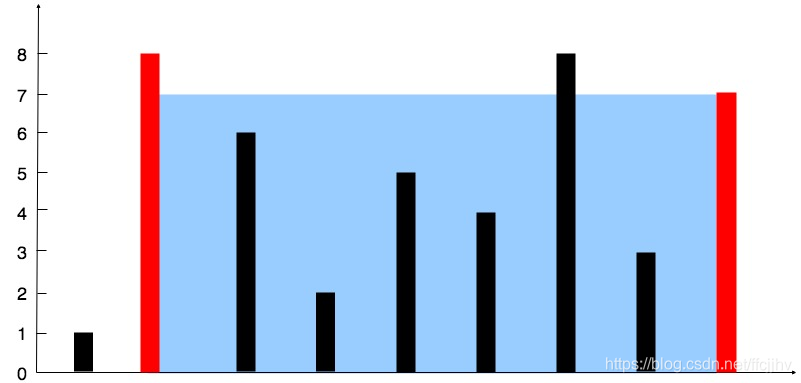
在这里插入图片描述
示例:

输入: [1,8,6,2,5,4,8,3,7]
输出: 49

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    // 时间复杂度：O(n)，空间复杂度：O(1)
    int maxArea(vector<int>& height) {
        int res=0;
        int i=0,j=height.size()-1;
        while(i<j){
            res = max(res,(j-i)*min(height[i],height[j]));
            if(height[i]<height[j]) i++;
            else j--;
        }
        return res;
    }
};

8、三数之和

给定一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？找出所有满足条件且不重复的三元组。

注意：答案中不可以包含重复的三元组。

例如, 给定数组 nums = [-1, 0, 1, 2, -1, -4]，

满足要求的三元组集合为：
[
[-1, 0, 1],
[-1, -1, 2]
]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    // 时间复杂度：O(n^2)，空间复杂度：O(1)
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> res;
        if(nums.empty()) return res;
        sort(nums.begin(),nums.end());
        for(int i=0;i<nums.size();i++){
            if(i>=1 && nums[i] == nums[i-1]) continue;
            if(nums[i]>0) break;
            int l=i+1,r=nums.size()-1;
            while(l<r){
                if(nums[l]+nums[r]+nums[i] < 0) l++;
                else if(nums[l]+nums[r]+nums[i] > 0) r--;
                else{
                    res.push_back({nums[i],nums[l],nums[r]});
                    l++;
                    r--;
                    while(l<r && nums[l]==nums[l-1]) l++;
                    while(l<r && nums[r]==nums[r+1]) r--;
                }
            }
        }
        return res;
    }
};

9、电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。
在这里插入图片描述
示例:

输入：”23”
输出：[“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”].
说明:
尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    // 时间复杂度：O(3^N*4^M)，空间复杂度：O(3^N*4^M)
    unordered_map<char,string> map{{'2',"abc"},{'3',"def"},{'4',"ghi"},{'5',"jkl"},{'6',"mno"},{'7',"pqrs"},{'8',"tuv"},{'9',"wxyz"}};

    vector<string> letterCombinations(string digits) {
        vector<string> res;
        if(digits.empty()) return res;
        help("",digits,res);
        return res;
    }

    void help(string str, string digits, vector<string> &res) {
        if(str.size() == digits.size()){
            res.push_back(str);
            return;
        }
        string tmp = map[digits[str.size()]];
        for(int i=0;i<tmp.size();i++){
            str += tmp[i];
            help(str,digits,res);
            str.pop_back();
        }
        return;
    }
};

注：可以联系剑指offer27题一起看

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    // 时间复杂度：O(3^N*4^M)，空间复杂度：O(3^N*4^M)
    vector<string> letterCombinations(string digits) {
        unordered_map<char,string> map{{'2',"abc"},{'3',"def"},{'4',"ghi"},{'5',"jkl"},{'6',"mno"},{'7',"pqrs"},{'8',"tuv"},{'9',"wxyz"}};
        vector<string> res;
        if(digits.empty()) return res;
        if(digits.size() == 1){
            string tmp = map[digits[0]];
            for(char w : tmp) {
                string s(1,w);
                res.push_back(s);
            }
            return res;
        }
        vector<string> last = letterCombinations(digits.substr(0,digits.size()-1));
        string tmp = map[digits[digits.size()-1]]; //abc def
        for(int i=0;i<last.size()||i==0;i++){
            for(int j=0;j<tmp.size();j++){
                res.push_back(last[i]+tmp[j]);
            }
        }
        return res;
    }
};

10、删除链表的倒数第N个节点

给定一个链表，删除链表的倒数第 n 个节点，并且返回链表的头结点。

示例：

给定一个链表: 1->2->3->4->5, 和 n = 2.

当删除了倒数第二个节点后，链表变为 1->2->3->5.
说明：

给定的 n 保证是有效的。

进阶：

你能尝试使用一趟扫描实现吗？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
	// 时间复杂度：O(n)，空间复杂度：O(1)
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        if(!head || n==0) return head;
        ListNode* l1 = head;
        ListNode* l2 = head;
        int k=0;
        while(l1){
            if(k>n) l2 = l2->next;
            l1 = l1->next;
            k++;
        }
        // 倒数第k-1个结点l2
        if(k == n) return head->next;
        l2->next = l2->next->next;
        return head;
    }
};

11、有效的括号

给定一个只包括 ‘(‘，’)’，’{‘，’}’，’[‘，’]’ 的字符串，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。

示例 1:

输入: “()”
输出: true
示例 2:

输入: “()[]{}”
输出: true
示例 3:

输入: “(]”
输出: false
示例 4:

输入: “([)]”
输出: false
示例 5:

输入: “{[]}”
输出: true

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
	// 时间复杂度：O(n)，空间复杂度：O(n)
    bool isValid(string s) {
        stack<char> stack;
        for(int i=0;i<s.size();i++){
            if(stack.empty() || !isok(stack.top(),s[i])){
                stack.push(s[i]);
            }
            else stack.pop();
        }
        return stack.empty();
    }

    bool isok(char a, char b) {
        return a=='('&&b==')' || a=='['&&b==']' || a=='{'&&b=='}';
    }
};

12、合并两个有序链表

将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例：

输入：1->2->4, 1->3->4
输出：1->1->2->3->4->4

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
	// 时间复杂度：O(n+m)，空间复杂度：O(1)
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        ListNode* res = new ListNode(0);
        ListNode* head = res;
        while(l1 && l2){
            if(l1->val<l2->val){
                head->next = l1;
                l1 = l1->next;
            }
            else{
                head->next = l2;
                l2 = l2->next;
            }
            head = head->next;
        }
        head->next = l1?l1:l2;
        return res->next;
    }
};

13、括号生成

给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。

例如，给出 n = 3，生成结果为：

[
“((()))”,
“(()())”,
“(())()”,
“()(())”,
“()()()”
]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    // 时间复杂度：O(4^n/sqrt(n))，空间复杂度：O(4^n/sqrt(n))
    vector<string> generateParenthesis(int n) {
        vector<string> res;
        if(n==0) return {""};
        for(int i=0;i<n;i++){
            vector<string> left = generateParenthesis(i);
            vector<string> right = generateParenthesis(n-1-i);
            for(string l :left){
                for(string r :right){
                    res.push_back("("+l+")"+r);
                }
            }
        }
        return res;
    }
};

14、合并K个排序链表

合并 k 个排序链表，返回合并后的排序链表。请分析和描述算法的复杂度。

示例:

输入:
[
1->4->5,
1->3->4,
2->6
] 输出: 1->1->2->3->4->4->5->6

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
	// 时间复杂度：O(Nlogk)，空间复杂度：O(1)
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        ListNode* res = NULL;
        for(int i=0;i<lists.size();i++){
            res = mergeTwoLists(res,lists[i]);
        }
        return res;
    }

    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        ListNode* res = new ListNode(0);
        ListNode* head = res;
        while(l1 && l2){
            if(l1->val<l2->val){
                head->next = l1;
                l1 = l1->next;
            }
            else{
                head->next = l2;
                l2 = l2->next;
            }
            head = head->next;
        }
        head->next = l1?l1:l2;
        return res->next;
    }
};

15、下一个排列

实现获取下一个排列的函数，算法需要将给定数字序列重新排列成字典序中下一个更大的排列。

如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。

必须原地修改，只允许使用额外常数空间。

以下是一些例子，输入位于左侧列，其相应输出位于右侧列。
1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
	// 时间复杂度：O(n)，空间复杂度：O(1)
    void nextPermutation(vector<int>& nums) {
        int i= nums.size()-2;
        while(i>=0 && nums[i]>=nums[i+1]){
            i--;
        }
        if(i>=0) {
            int j = nums.size()-1;
            while(j>=0 && nums[j]<=nums[i]){
                j--;
            }
            swap(nums[i],nums[j]);
        }
        reverse(nums,i+1);
    }

    void reverse(vector<int>& nums,int n){
        int l=n,r=nums.size()-1;
        while(l<r){
            swap(nums[l],nums[r]);
            l++;
            r--;
        }
    }
};

16、最长有效括号

给定一个只包含 ‘(‘ 和 ‘)’ 的字符串，找出最长的包含有效括号的子串的长度。

示例 1:

输入: “(()”
输出: 2
解释: 最长有效括号子串为 “()”
示例 2:

输入: “)()())”
输出: 4
解释: 最长有效括号子串为 “()()”

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
	// 时间复杂度：O(n)，空间复杂度：O(1)
    int longestValidParentheses(string s) {
        int l = 0, r = 0 , res = 0;
        for(int i=0;i<s.size();i++){
            if(s[i] == '(') l++;
            if(s[i] == ')') r++;
            if(l==r) res = max(res,2*l);
            if(r>l) l=r=0;
        }
        l=0,r=0;
        for(int i=s.size()-1;i>=0;i--){
            if(s[i] == '(') l++;
            if(s[i] == ')') r++;
            if(l==r) res = max(res,2*l);
            if(l>r) l=r=0;
        }
        return res;
    }
};

17、搜索旋转排序数组

假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。

搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。

你可以假设数组中不存在重复的元素。

你的算法时间复杂度必须是 O(log n) 级别。

示例 1:

输入: nums = [4,5,6,7,0,1,2], target = 0
输出: 4
示例 2:

输入: nums = [4,5,6,7,0,1,2], target = 3
输出: -1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
	// 时间复杂度：O(logN)，空间复杂度：O(1)
    int search(vector<int>& nums, int target) {
        return help(nums,target,0,nums.size()-1);
    }
    int help(vector<int>& nums, int target, int l, int r) {
        if(l>r) return -1;
        int mid = (l+r)/2;
        if(nums[mid] == target) return mid;
        if(nums[mid]>nums[r]){ // 3 4 7 8 1 2  旋转点在右，左顺序
            if(nums[l]<=target && target <nums[mid]) return help(nums,target,l,mid-1);
            else return help(nums,target,mid+1,r);
        }
        else{ // 7 8 1 2 3 4
            if(nums[mid]<target && target <=nums[r]) return help(nums,target,mid+1,r);
            else return help(nums,target,l,mid-1);
        }
    }
};

18、在排序数组中查找元素的第一个和最后一个位置

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

你的算法时间复杂度必须是 O(log n) 级别。

如果数组中不存在目标值，返回 [-1, -1]。

示例 1:

输入: nums = [5,7,7,8,8,10], target = 8
输出: [3,4]
示例 2:

输入: nums = [5,7,7,8,8,10], target = 6
输出: [-1,-1]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
	// 时间复杂度：O(logN)，空间复杂度：O(1)
    vector<int> searchRange(vector<int>& nums, int target) {
        vector<int> res{-1,-1};
        int l=0,r=nums.size()-1;
        while(l<=r){
            int mid=(l+r)/2;
            if(nums[mid] == target) {
                help(nums,mid,res);
                break;
            }
            else if(nums[mid] > target) r = mid-1;
            else l = mid+1;
        }
        return res;
    }
    void help(vector<int> nums, int n,vector<int> &res) {
        int l=n,r=n;
        while(l>=0&&nums[l]==nums[n]){
            l--;
        }
        while(r<nums.size()&&nums[r]==nums[n]){
            r++;
        }
        res[0]=l+1;
        res[1]=r-1;
    }
};

19、组合总和

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。

说明：
所有数字（包括 target）都是正整数。
解集不能包含重复的组合。
示例 1:

输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
] 示例 2:

输入: candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        sort(candidates.begin(),candidates.end());
        vector<vector<int>> res;
        vector<int> path;
        dfs(candidates,target,0,path,res);
        return res;
    }
    void dfs(vector<int>& candidates, int target, int start, vector<int> &path, vector<vector<int>> &res) {
        if(target == 0) {
            res.push_back(path);
            return;
        }
        for(int i=start;i<candidates.size()&&target>=candidates[i];i++){
            path.push_back(candidates[i]);
            dfs(candidates,target-candidates[i],i,path,res);
            path.pop_back();
        }
    }
};

20、接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
在这里插入图片描述
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。

示例:

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    // 时间复杂度：O(n)，空间复杂度：O(1)
    int trap(vector<int>& height) {
        int res = 0;
        int l = 0, r = height.size()-1;
        int max_left = 0, max_right = 0;
        while(l<r){
            if(height[l]<height[r]){
                if(height[l]>=max_left) max_left = height[l];
                else res += max_left-height[l];
                l++;
            }
            else{
                if(height[r]>=max_right) max_right = height[r];
                else res += max_right-height[r];
                r--;
            }
        }
        return res;
    }
};

21、全排列

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    // 时间复杂度：O(n!)，空间复杂度：O(1)
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> res;
        help(nums,res,0);
        return res;
    }
    void help(vector<int>& nums, vector<vector<int>> &res, int k){
        if(k==nums.size()-1) res.push_back(nums);
        for(int i=k;i<nums.size();i++){
            swap(nums[i],nums[k]);
            help(nums,res,k+1);
            swap(nums[i],nums[k]);
        }
    }
};

22、旋转图像

给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度。

说明：
你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

示例 1:

给定 matrix =
[
[1,2,3],
[4,5,6],
[7,8,9]
],

原地旋转输入矩阵，使其变为:
[
[7,4,1],
[8,5,2],
[9,6,3]
] 示例 2:

给定 matrix =
[
[ 5, 1, 9,11],
[ 2, 4, 8,10],
[13, 3, 6, 7],
[15,14,12,16]
],

原地旋转输入矩阵，使其变为:
[
[15,13, 2, 5],
[14, 3, 4, 1],
[12, 6, 8, 9],
[16, 7,10,11]
]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    // 时间复杂度：O(n^2)，空间复杂度：O(1)
    void rotate(vector<vector<int>>& matrix) {
        int n= matrix.size();
        for(int i=0;i<n;i++){
            for(int j=i;j<n;j++){
                swap(matrix[i][j],matrix[j][i]);
            }
        }
        for(int i=0;i<n;i++){
            for(int j=0;j<n/2;j++){
                swap(matrix[i][j],matrix[i][n-1-j]);
            }
        }
    }
};

23、字母异位词分组

给定一个字符串数组，将字母异位词组合在一起。字母异位词指字母相同，但排列不同的字符串。

示例:

输入: [“eat”, “tea”, “tan”, “ate”, “nat”, “bat”],
输出:
[
[“ate”,”eat”,”tea”],
[“nat”,”tan”],
[“bat”]
] 说明：

所有输入均为小写字母。
不考虑答案输出的顺序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
	// 时间复杂度：O(NK)，空间复杂度：O(NK)
    vector<vector<string>> groupAnagrams(vector<string>& strs) {
        unordered_map<string,int> map;
        vector<vector<string>> res;
        int k = 0;
        for(int i=0;i<strs.size();i++){
            string str = strs[i];
            string node(26,'0'); 
            for(int j=0;j<str.size();j++){
                int t = node[str[j]-'a']-'0'+1;
                node[str[j]-'a']= '0' + t;
            }
            if(map.find(node)!=map.end()){
                res[map[node]].push_back(str);
            }
            else{
                map[node] = k;
                res.push_back(vector<string>{str});
                k++;
            }
        }
        return res;
    }
};

24、最大子序和

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。
进阶:

如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    // 时间复杂度：O(n)，空间复杂度：O(1)
    int maxSubArray(vector<int>& nums) {
        int res = INT_MIN;
        int add = 0;
        for(int i=0;i<nums.size();i++){
            add+=nums[i];
            res=max(res,add);
            if(add<0) add=0;
        }
        return res;
    }
};

25、跳跃游戏

给定一个非负整数数组，你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个位置。

示例 1:

输入: [2,3,1,1,4]
输出: true
解释: 我们可以先跳 1 步，从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
示例 2:

输入: [3,2,1,0,4]
输出: false
解释: 无论怎样，你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 ， 所以你永远不可能到达最后一个位置。

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    // 时间复杂度：O(n)，空间复杂度：O(1)
    bool canJump(vector<int>& nums) {
       int last = nums.size()-1;
       for(int i=nums.size()-2;i>=0;i--){
           if(i+nums[i]>=last) last = i;
       }
       return last == 0;
    }
};

26、合并区间

给出一个区间的集合，请合并所有重叠的区间。

示例 1:

输入: [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:

输入: [[1,4],[4,5]]
输出: [[1,5]]
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
	// 时间复杂度：O(nlogn)，空间复杂度：O(1)
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        vector<vector<int>> res;
        sort(intervals.begin(),intervals.end(),Sort);
        for(int i=0;i<intervals.size();i++){
            if(res.empty() || intervals[i][0]>res[res.size()-1][1])
                res.push_back(intervals[i]);
            else
                res[res.size()-1][1] = max(res[res.size()-1][1],intervals[i][1]);
        }
        return res;
    }
    static bool Sort(vector<int> &a,vector<int> &b) {
        return a[0]<b[0];
    }
};

27、不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。
问总共有多少条不同的路径？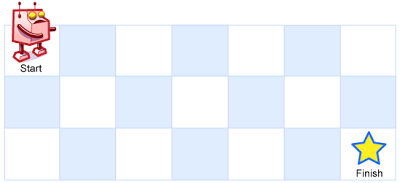
在这里插入图片描述
例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。

  1. 向右 -> 向右 -> 向下
  2. 向右 -> 向下 -> 向右
  3. 向下 -> 向右 -> 向右
    示例 2:

输入: m = 7, n = 3
输出: 28

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
	// 时间复杂度：O(nm)，空间复杂度：O(nm)
    int uniquePaths(int m, int n) {
        vector<vector<int>> dp(m+1,vector<int>(n+1));
        dp[0][0] = 0;
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(i==1||j==1) dp[i][j] = 1;
                else dp[i][j] = dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m][n];
    }
};

28、最小路径和

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例:

输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
] 输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
	// 时间复杂度：O(nm)，空间复杂度：O(nm)
    int minPathSum(vector<vector<int>>& grid) {
        int res = INT_MAX;
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> dp(m,vector<int>(n,0));
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(i==0&&j==0) dp[i][j] = grid[i][j];
                else{
                    if(i==0) dp[i][j] = dp[i][j-1] + grid[i][j];
                    else if(j==0) dp[i][j] = dp[i-1][j] + grid[i][j];
                    else dp[i][j] = min(dp[i][j-1],dp[i-1][j]) + grid[i][j];
                }
            }
        }
        return dp[m-1][n-1];
    }
};

29、爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。

  1. 1 阶 + 1 阶
  2. 2 阶
    示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。

  1. 1 阶 + 1 阶 + 1 阶
  2. 1 阶 + 2 阶
  3. 2 阶 + 1 阶
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
	// 时间复杂度：O(n)，空间复杂度：O(1)
    int climbStairs(int n) {
        // 1 2 3 5
        int i=0,j=1,k=0;
        while(k<n){
            int t = j;
            j = i+j;
            i = t;
            k++;
        }
        return j;
    }
};

30、编辑距离

给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符
示例 1:

输入: word1 = “horse”, word2 = “ros”
输出: 3
解释:
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)
示例 2:

输入: word1 = “intention”, word2 = “execution”
输出: 5
解释:
intention -> inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
	// 时间复杂度：O(mn)，空间复杂度：O(mn)
    int minDistance(string word1, string word2) {
        int m= word1.size(), n=word2.size();
        vector<vector<int>> dp(m+1,vector<int>(n+1));
        for(int i=0;i<=m;i++){
            for(int j=0;j<=n;j++){
                if(i==0||j==0) dp[i][j]= max(i,j);
                else if(word1[i-1]==word2[j-1]) dp[i][j] = dp[i-1][j-1];
                else dp[i][j]= min(dp[i-1][j],min(dp[i][j-1],dp[i-1][j-1])) + 1;
            }
        }
        return dp[m][n];
    }
};

31、颜色分类

给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

注意:
不能使用代码库中的排序函数来解决这道题。

示例:

输入: [2,0,2,1,1,0]
输出: [0,0,1,1,2,2]
进阶：

一个直观的解决方案是使用计数排序的两趟扫描算法。
首先，迭代计算出0、1 和 2 元素的个数，然后按照0、1、2的排序，重写当前数组。
你能想出一个仅使用常数空间的一趟扫描算法吗？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
	// 时间复杂度：O(n)，空间复杂度：O(1)
    void sortColors(vector<int>& nums) {
        int p0 = 0, p2 = nums.size()-1, cur = 0;
        while(cur<=p2){
            if(nums[cur] == 0){
                swap(nums[p0],nums[cur]); 
                p0++;
                cur++;
            }
            else if(nums[cur] == 2){
                swap(nums[p2],nums[cur]); 
                p2--;
            }
            else cur++;
        }
    }
};

32、最小覆盖子串

给你一个字符串 S、一个字符串 T，请在字符串 S 里面找出：包含 T 所有字母的最小子串。

示例：

输入: S = “ADOBECODEBANC”, T = “ABC”
输出: “BANC”
说明：

如果 S 中不存这样的子串，则返回空字符串 “”。
如果 S 中存在这样的子串，我们保证它是唯一的答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
	// 时间复杂度：O(S+T)，空间复杂度：O(S+T)
    string minWindow(string s, string t) {
        int start = 0, len = INT_MAX;
        int l = 0, r = 0;
        unordered_map<char,int> map;
        unordered_map<char,int> match;
        for(char c : t) map[c]++;
        
        int count = 0;
        while(r<s.size()){
            char t = s[r];
            if(map.count(t)){
                match[t]++;
                if(map[t] == match[t]){
                    count++;
                }
            }
            r++;

            while(map.size()==count){
                if(r-l<len){
                    start = l;
                    len = r-l;
                }
                char t2 = s[l];
                if(map.count(t2)){
                    match[t2]--;
                    if(match[t2]<map[t2]){
                        count--;
                    }
                }
                l++;
            }
        }
        return len == INT_MAX? "":s.substr(start,len);
    }
};

33、子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    // 利用二进制，时间复杂度：O(2^n)，空间复杂度：O(2^n)
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> res;
        int len = 1<<nums.size();
        for(int i=0;i<len;i++){
            vector<int> tmp;
            for(int j=0;j<nums.size();j++){
                if(i&(1<<j)) tmp.push_back(nums[j]);
            }
            res.push_back(tmp);
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
	// 时间复杂度：O(2^n)，空间复杂度：O(2^n)
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> res{{}};
        for(int i=0;i<nums.size();i++){
            int len = res.size();
            for(int j=0;j<len;j++){
                vector<int> tmp(res[j]);
                tmp.push_back(nums[i]);
                res.push_back(tmp);
            }
        }
        return res;
    }
};

34、单词搜索

给定一个二维网格和一个单词，找出该单词是否存在于网格中。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例:

board =
[
[‘A’,’B’,’C’,’E’],
[‘S’,’F’,’C’,’S’],
[‘A’,’D’,’E’,’E’]
]

给定 word = “ABCCED”, 返回 true.
给定 word = “SEE”, 返回 true.
给定 word = “ABCB”, 返回 false.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {
        for(int i=0;i<board.size();i++){
            for(int j=0;j<board[0].size();j++){
                if(help(board,i,j,word,0)) return true;
            }
        }
        return false;
    }
    bool help(vector<vector<char>> &board, int i, int j, string word, int k) {
        if(i<0||i>=board.size()||j<0||j>=board[0].size()||board[i][j]=='*'||board[i][j]!=word[k]) return false;
        if(k==word.size()-1) return true;
        char tmp = board[i][j];
        board[i][j] = '*';
        if(help(board,i-1,j,word,k+1)
        || help(board,i+1,j,word,k+1)
        || help(board,i,j-1,word,k+1)
        || help(board,i,j+1,word,k+1)){
            return true;
        }
        board[i][j] = tmp;
        return false;
    }
};

35、柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。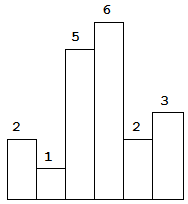
在这里插入图片描述
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。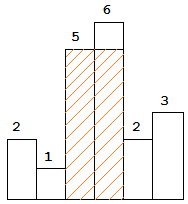
在这里插入图片描述
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    // 时间复杂度：O(nlogn)，空间复杂度：O(n) 有时候通过有时候超时
    int largestRectangleArea(vector<int>& heights) {
        return help(heights,0,heights.size()-1);
    }
    int help(vector<int> &heights, int l, int r){
        if(l>r) return 0;
        int low = l;
        for(int i=l;i<=r;i++){
            if(heights[i]<heights[low]) low = i;
        }
        return max(heights[low]*(r-l+1),max(help(heights,l,low-1),help(heights,low+1,r)));
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    // 时间复杂度：O(n)，空间复杂度：O(n)
    int largestRectangleArea(vector<int>& heights) {        
        stack<int> st;
        heights.push_back(0);
        int size = heights.size();
        int res = 0;
        for (int i = 0; i < size; i++) {
            while (!st.empty() && heights[st.top()] >= heights[i]) {
                int val = st.top();
                st.pop();
                res = max(res, heights[val] * (st.empty() ? i : (i - st.top() - 1)));
            }
            st.push(i);
        }
        return res;
    } 
};

36、最大矩形

给定一个仅包含 0 和 1 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例:

输入:
[
[“1”,”0”,”1”,”0”,”0”],
[“1”,”0”,”1”,”1”,”1”],
[“1”,”1”,”1”,”1”,”1”],
[“1”,”0”,”0”,”1”,”0”]
] 输出: 6

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
	// 时间复杂度：O(n*m)，空间复杂度：O(m)
    int maximalRectangle(vector<vector<char>>& matrix) {
        if(matrix.empty()) return 0;
        int res = 0;
        vector<int> vec(matrix[0].size(),0);
        for(int i=0;i<matrix.size();i++){
            for(int j=0;j<matrix[0].size();j++){
                vec[j] = matrix[i][j]=='1'?vec[j]+1:0;
            }
            res = max(res,help(vec));
        }
        return res;
    }
    int help(vector<int> &vec){
        stack<int> stack;
        int res = 0;
        vec.push_back(0);
        for(int i=0;i<vec.size();i++){
            while(!stack.empty()&&vec[stack.top()]>=vec[i]){
                int tmp = stack.top();
                stack.pop();
                res = max(res,vec[tmp]*(stack.empty()?i:(i-stack.top()-1)));
            }
            stack.push(i);
        }
        vec.pop_back();
        return res;
    }
};

37、二叉树的中序遍历

给定一个二叉树，返回它的中序 遍历。

示例:

输入: [1,null,2,3]

1
2
3
4
5
1
 \
  2
 /
3

输出: [1,3,2]
进阶: 递归算法很简单，你可以通过迭代算法完成吗？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    // 时间复杂度：O(n)，空间复杂度：O(logn) 递归
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        help(res,root);
        return res;
    }
    void help(vector<int> &res, TreeNode* root){
        if(!root) return;
        help(res,root->left);
        res.push_back(root->val);
        help(res,root->right);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    // 时间复杂度：O(n)，空间复杂度：O(n) 栈
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> stack;
        TreeNode* cur = root;
        while(cur || !stack.empty()){
            while(cur){
                stack.push(cur);
                cur = cur->left;
            }
            cur = stack.top();
            stack.pop();
            res.push_back(cur->val);
            cur = cur->right;
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    // 时间复杂度：O(n)，空间复杂度：O(n) 线索二叉树
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        TreeNode* cur = root;
        TreeNode* next;
        while(cur){
            if(!cur->left){
                res.push_back(cur->val);
                cur = cur->right;
            }
            else{
                next = cur->left;
                while(next->right){
                    next = next->right;
                }
                next->right = cur;
                TreeNode* tmp = cur;
                cur = cur->left;
                tmp->left = NULL;
            }
        }
        return res;
    }
};

38、不同的二叉搜索树

给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种？

示例:

输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:

1
2
3
4
5
1         3     3      2      1
 \       /     /      / \      \
  3     2     1      1   3      2
 /     /       \                 \
2     1         2                 3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    // 时间复杂度：O(n^2)，空间复杂度：O(n)
    int numTrees(int n) {
        vector<int> res(n+1);
        res[0] = 1;
        res[1] = 1;
        for(int i=2;i<=n;i++){
            for(int j=1;j<=i;j++){
                res[i] += res[j-1]*res[i-j];
            }
        }
        return res[n];
    }
};

39、验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:

输入:

1
2
3
  2
 /  \
1    3

输出: true
示例 2:

输入:

1
2
3
4
5
  5
 /  \
1    4
    /  \
    3   6

输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
根节点的值为 5 ，但是其右子节点值为 4 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    // 时间复杂度：O(n)，空间复杂度：O(n) 中序遍历递增
    bool isValidBST(TreeNode* root) {
        stack<TreeNode*> stack;
        TreeNode* cur = root;
        //int tmp = INT_MIN; // 测试用例用[-2147483648]卡边界值过分了。。。
        long tmp = LONG_MIN;
        while(cur || !stack.empty()){
            while(cur){
                stack.push(cur);
                cur=cur->left;
            }
            cur = stack.top();
            stack.pop();
            if(cur->val<=tmp){
                return false;
            }
            tmp = cur->val;
            cur = cur->right;
        }
        return true;
    }
};

40、对称二叉树

给定一个二叉树，检查它是否是镜像对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

1
2
3
4
5
    1
   / \
  2   2
 / \ / \
3  4 4  3

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

1
2
3
4
5
  1
 / \
2   2
 \   \
 3    3

说明:

如果你可以运用递归和迭代两种方法解决这个问题，会很加分。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
	// 时间复杂度：O(n)，空间复杂度：O(n) 递归
    bool isSymmetric(TreeNode* root) {
        if(!root) return true;
        return help(root->left,root->right);
    }
    bool help(TreeNode* l,TreeNode* r) {
        if(!l && !r) return true;
        if(!l || !r) return false;
        return l->val==r->val && help(l->right,r->left) && help(l->left,r->right);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
	// 时间复杂度：O(n)，空间复杂度：O(n) 迭代
    bool isSymmetric(TreeNode* root) {
        queue<TreeNode*> queue;
        queue.push(root);
        queue.push(root);
        while(!queue.empty()){
            TreeNode* t1 = queue.front();
            queue.pop();
            TreeNode* t2 = queue.front();
            queue.pop();
            if(!t1 && !t2) continue;
            if(!t1 || !t2) return false;
            if(t1->val != t2->val) return false;
            queue.push(t1->left);
            queue.push(t2->right);
            queue.push(t2->left);
            queue.push(t1->right);
        }
        return true;
    }
};

41、二叉树的层次遍历

给定一个二叉树，返回其按层次遍历的节点值。 （即逐层地，从左到右访问所有节点）。

例如:
给定二叉树: [3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回其层次遍历结果：

1
2
3
4
5
[
  [3],
  [9,20],
  [15,7]
]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
	// 时间复杂度：O(n)，空间复杂度：O(n) 
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> res;
        queue<TreeNode*> queue;
        if(root) queue.push(root);
        while(!queue.empty()){
            int count = queue.size();
            vector<int> tmp;
            while(count!=0){
                tmp.push_back(queue.front()->val);
                count--;
                if(queue.front()->left) queue.push(queue.front()->left);
                if(queue.front()->right) queue.push(queue.front()->right);
                queue.pop();
            }
            res.push_back(tmp);
        }
        return res;
        
    }
};

42、二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

返回它的最大深度 3 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
	// 时间复杂度：O(n)，空间复杂度：O(logn) 
    int maxDepth(TreeNode* root) {
        if(!root) return 0;
        return max(maxDepth(root->left),maxDepth(root->right))+1;
    }
};

43、从前序与中序遍历序列构造二叉树

根据一棵树的前序遍历与中序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树：

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7·
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
	// 时间复杂度：O(n)，空间复杂度：O(n) 
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        return help(preorder,0,preorder.size()-1,inorder,0,inorder.size()-1);
    }
    TreeNode* help(vector<int>& pre,int pl,int pr,vector<int>& vin,int vl,int vr) {
        if(pl>pr || vl>vr) return NULL;
        TreeNode* head = new TreeNode(pre[pl]);
        int i;
        for(i=vl;i<=vr;i++){
            if(vin[i]==pre[pl]) break;
        }
        int num = i-vl;
        head->left=help(pre,pl+1,pl+num,vin,vl,vl+num-1);
        head->right=help(pre,pl+num+1,pr,vin,vl+num+1,vr);
        return head;
    }
};

44、二叉树展开为链表

给定一个二叉树，原地将它展开为链表。

例如，给定二叉树

1
2
3
4
5
    1
   / \
  2   5
 / \   \
3   4   6

将其展开为：

1
2
3
4
5
6
7
8
9
10
11
1
 \
  2
   \
    3
     \
      4
       \
        5
         \
          6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    // 先序遍历 线索二叉树
    // 时间复杂度：O(n)，空间复杂度：O(1) 
    void flatten(TreeNode* root) {
        TreeNode* cur = root;
        TreeNode* next;
        while(cur){
            if(!cur->left){
                cur = cur->right;
            }
            else{
                next = cur->left;
                while(next->right){
                    next = next->right;
                }
                next->right = cur->right;
                cur->right = cur->left;
                cur->left = NULL;
                cur = cur->right;
            }
        }
    }
    /*
    // 中序遍历 线索二叉树
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        TreeNode* cur = root;
        TreeNode* next;
        while(cur){
            if(!cur->left){
                res.push_back(cur->val);
                cur = cur->right;
            }
            else{
                next = cur->left;
                while(next->right){
                    next = next->right;
                }
                next->right = cur;
                TreeNode* tmp = cur;
                cur = cur->left;
                tmp->left = NULL;
            }
        }
        return res;
    }
    */
};

45、买卖股票的最佳时机

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。

注意你不能在买入股票前卖出股票。

示例 1:

输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
示例 2:

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
	// 时间复杂度：O(n)，空间复杂度：O(1) 
    int maxProfit(vector<int>& prices) {
        int res = 0;
        int minp = INT_MAX;
        for(int i=0;i<prices.size();i++){
            minp=min(minp,prices[i]);
            res = max(res,prices[i]-minp);
        }
        return res;
    }
};

46、二叉树中的最大路径和

给定一个非空二叉树，返回其最大路径和。

本题中，路径被定义为一条从树中任意节点出发，达到任意节点的序列。该路径至少包含一个节点，且不一定经过根节点。

示例 1:

输入: [1,2,3]

  1
 / \
2   3

输出: 6
示例 2:

输入: [-10,9,20,null,null,15,7]

-10
/
9 20
/
15 7

输出: 42

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
	// 时间复杂度：O(n)，空间复杂度：O(logn) 
    int maxPathSum(TreeNode* root) {
        int res=INT_MIN;
        help(root,res);
        return res;
    }
    int help(TreeNode* root,int &res){ // 从root向下走的最长距离
        if(!root) return 0;
        int l = max(0, help(root->left,res));
        int r = max(0, help(root->right,res));
        res = max(res,root->val+l+r);
        return root->val+max(l,r);
    }
};

47、最长连续序列

给定一个未排序的整数数组，找出最长连续序列的长度。

要求算法的时间复杂度为 O(n)。

示例:

输入: [100, 4, 200, 1, 3, 2]
输出: 4
解释: 最长连续序列是 [1, 2, 3, 4]。它的长度为 4。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
	// 时间复杂度：O(n)，空间复杂度：O(n) 
    int longestConsecutive(vector<int>& nums) {
        int res = 0;
        set<int> s(nums.begin(),nums.end());
        set<int>::iterator it;
        for(it = s.begin();it!=s.end();it++){
            int beg = *it;
            if(s.find(beg-1)==s.end()){
                int len = 1;
                while(s.find(beg+1)!=s.end()){
                    len++;
                    beg++;
                }
                res=max(res,len);
            }
        }
        return res;
    }
};

48、只出现一次的数字

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例 1:

输入: [2,2,1]
输出: 1
示例 2:

输入: [4,1,2,1,2]
输出: 4

1
2
3
4
5
6
7
8
9
class Solution {
public:
	// 时间复杂度：O(n)，空间复杂度：O(1) 
    int singleNumber(vector<int>& nums) {
        int res;
        for(int num:nums) res^=num;
        return res;
    }
};

49、单词拆分

给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

说明：

拆分时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。
示例 1：

输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true
解释: 返回 true 因为 “leetcode” 可以被拆分成 “leet code”。
示例 2：

输入: s = “applepenapple”, wordDict = [“apple”, “pen”]
输出: true
解释: 返回 true 因为 “applepenapple” 可以被拆分成 “apple pen apple”。
注意你可以重复使用字典中的单词。
示例 3：

输入: s = “catsandog”, wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
输出: false

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
	// 时间复杂度：O(n^2)，空间复杂度：O(n) 
    // dp[i]表示字符串s的前i个字符能否拆分成wordDict
    bool wordBreak(string s, vector<string>& wordDict) {
        vector<bool> flag(s.size()+1,false);
        unordered_set<string> set(wordDict.begin(),wordDict.end());
        flag[0] = true;
        for(int i=1;i<=s.size();i++){
            for(int j=0;j<i;j++){
                if(flag[j] && set.find(s.substr(j,i-j))!=set.end()){
                    flag[i]=true;
                    break;
                }
            }
        }
        return flag[s.size()];
    }
};

50、环形链表

给定一个链表，判断链表中是否有环。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。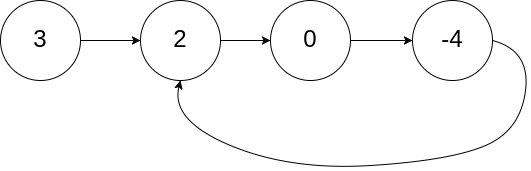
在这里插入图片描述
示例 2：

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。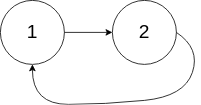
在这里插入图片描述
示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。
在这里插入图片描述
进阶：

你能用 O(1)（即，常量）内存解决此问题吗？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
	// 时间复杂度：O(n)，空间复杂度：O(1) 
    bool hasCycle(ListNode *head) {
        if(!head) return false;
        ListNode * fast = head;
        ListNode * slow = head;
        while(fast && fast->next){
            fast = fast->next->next;
            slow = slow->next;
            if(fast == slow) return true;
        }
        return false;
    }
};
0%