常见算法的c++实现总结

发表于 | 分类于 ， ， | 阅读次数:

目录

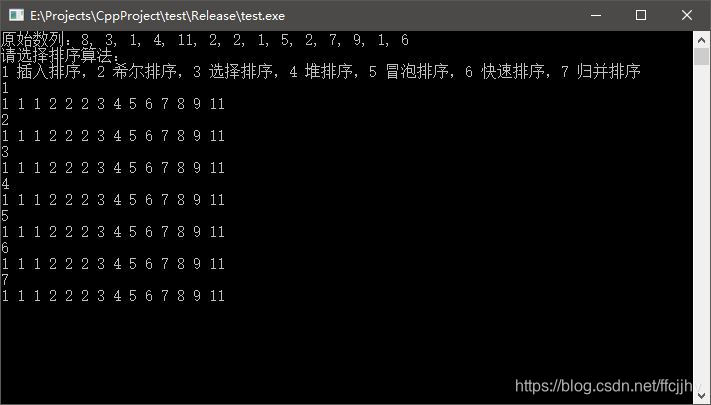
一、七大排序算法
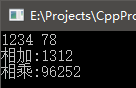
二、大整数计算
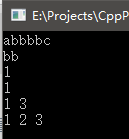
三、编kmp辑距离问题
四、kmp算法
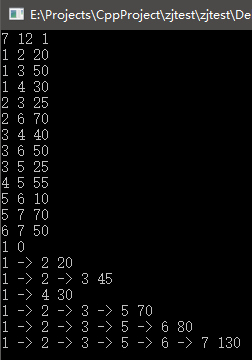
五、dijkstra算法
六、0/1背包问题

一、七大排序算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
#include <iostream>
#include <vector>
using namespace std;

void swap(int &a, int &b) {
	int tmp;
	tmp = a;
	a = b;
	b = tmp;
}

//一、插入排序
//1.1 直接插入排序  时间复杂度O(n^2)  空间复杂度O(1)  稳定
//构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。
void insert_sort(vector<int> &nums) {
	for (int i = 0; i < nums.size(); i++){
		for (int j = i; j > 0; j--){
			if (nums[j] < nums[j - 1])
				swap(nums[j], nums[j - 1]);
		}
	}
}

//1.2 希尔排序  时间复杂度O(n^1.3)  空间复杂度O(1)  不稳定
//按照一定步长分成子序列进行排序，然后逐步递减步长来完成最终排序。增量 d = 1时， 就是插入排序
void shell_sort(vector<int> &nums) {
	for (int gap = nums.size() >> 1; gap>0; gap >>= 1){
		for (int i = gap; i < nums.size(); i++)
		{
			int tmp = nums[i];
			int j = i - gap;
			for (; j >= 0 && nums[j] > tmp; j -= gap){
				nums[j + gap] = nums[j];
			}
			nums[j + gap] = tmp;
		}
	}
}

//二、选择排序
//2.1 选择排序  时间复杂度O(n^2)  空间复杂度O(1)  不稳定
//先进行第一轮循环比较相邻两项，找到最小值得下标，将最小值与第一项交换，然后重复排序剩余部分。
void select_sort(vector<int> &nums) {
	for (int i = 0; i < nums.size(); i++) {
		int min = i;
		for (int j = i + 1; j < nums.size(); j++){
			if (nums[j] < nums[min])
				min = j;
		}
		swap(nums[i], nums[min]);
	}
}

//2.2 堆排序  时间复杂度O(nlgn)  空间复杂度O(1)  稳定
//构造一个最大堆（完全二叉树），父结点大于左右子结点，然后取出根结点（最大值）与最后一个结点交换，重复调整剩余的结点成最大堆，得到有序的序列。
void max_heapify(vector<int> &nums, int l, int r) {
	int curr = l;
	int child = curr * 2 + 1;
	while (child < r) {
		if (child + 1 < r &&nums[child] < nums[child + 1])
			child++;
		if (nums[curr] < nums[child]) {
			swap(nums[curr], nums[child]);
			curr = child;
			child = 2 * curr + 1;
		}
		else
			break;
	}
}

void heap_sort(vector<int> &nums) {
	for (int i = nums.size() / 2 - 1; i >= 0; i--)
	{
		max_heapify(nums, i, nums.size());
	}
	for (int i = nums.size() - 1; i > 0; i--)
	{
		swap(nums[0], nums[i]);
		max_heapify(nums, 0, i);
	}
}


//三、交换排序
//3.1 冒泡排序  时间复杂度O(n^2)  空间复杂度O(1)  稳定
//每次通过两两比较交换位置，选出剩余无序序列里最大（小）的数据元素放到队尾。
void bubble_sort(vector<int> &nums) {
	for (int i = 0; i < nums.size() - 1; i++){
		for (int j = 0; j < nums.size() - i - 1; j++){
			if (nums[j] > nums[j + 1])
				swap(nums[j], nums[j + 1]);
		}
	}
}

//3.2快速排序  时间复杂度O(nlgn)  空间复杂度O(1)  不稳定
//将无序序列分隔成两部分，左边均比右边小，分别对这两部分进行排序
void quick_sort(vector<int> &nums, int l, int r) {
	if (l < r) {
		int i = l, j = r;
		while (i < j) {
			while (nums[j] >= nums[l] && i < j)
				j--;
			while (nums[i] <= nums[l] && i < j)
				i++;
			swap(nums[i], nums[j]);
		}
		swap(nums[l], nums[i]);
		quick_sort(nums, l, i-1);
		quick_sort(nums, i + 1, r);
	}
}

//四、归并排序  时间复杂度O(nlgn)  空间复杂度O(n)  稳定
//将序列递归分成单位为1的小序列，然后两两合并排序，最终得到有序的序列。
void  merge_sort(vector<int> &nums, int l, int r, vector<int> &tmp) {
	if (l >= r) return;
	int m = (l + r) / 2;
	merge_sort(nums, l, m, tmp);
	merge_sort(nums, m + 1, r, tmp);
	int i = l, j = m + 1, index = l;
	while (i <= m &&  j <= r) {
		if (nums[i] < nums[j])
			tmp[index++] = nums[i++];
		else
			tmp[index++] = nums[j++];
	}
	while (i <= m)
		tmp[index++] = nums[i++];
	while (j <= r)
		tmp[index++] = nums[j++];
	for (int i = l; i <= r; i++)
		nums[i] = tmp[i];
}


int main() {

	cout << "原始数列：8, 3, 1, 4, 11, 2, 2, 1, 5, 2, 7, 9, 1, 6 " << endl;
	cout << "请选择排序算法：" << endl;
	cout << "1 插入排序，2 希尔排序，3 选择排序，4 堆排序，5 冒泡排序，6 快速排序，7 归并排序" << endl;

	int index;
	while (cin >> index){
		vector<int> nums{ 8, 3, 1, 4, 11, 2, 2, 1, 5, 2, 7, 9, 1, 6 };
		int len = nums.size();
		switch (index){
		case 1:
			insert_sort(nums); //插入排序
			break;
		case 2:
			shell_sort(nums); //希尔排序
			break;
		case 3:
			select_sort(nums); //选择排序
			break;
		case 4:
			heap_sort(nums); //堆排序
			break;
		case 5:
			bubble_sort(nums); //冒泡排序
			break;
		case 6:
			quick_sort(nums, 0, len - 1); //快速排序
			break;
		case 7:
			vector<int> tmp(len);
			merge_sort(nums, 0, len - 1, tmp); //归并排序
			break;
		}

		for (int i = 0; i<nums.size(); i++){
			cout << nums[i] << ' ';
		}
		cout << endl;
	}
	return 0;
}

在这里插入图片描述

二、大整数计算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <iostream>
#include <string>
using namespace std;

//大数相加
string addstr(string s1, string s2) {
	if (s1.size()>s2.size()) return addstr(s2, s1); //s1短
	s1.insert(s1.begin(), s2.size() - s1.size(), '0');
	string res(s2.size() + 1, '0');
	for (int i = s2.size() - 1; i >= 0; i--){
		int t = (s1[i] - '0') + (s2[i] - '0') + (res[i + 1] - '0');
		res[i + 1] = t % 10 + '0';
		res[i] = t / 10 + '0';
	}
	if (res[0] == '0') return res.substr(1);
	return res;
}
//大数相乘
string multiply(string num1, string num2) {
	int len1 = num1.size(), len2 = num2.size();
	string res(len1 + len2, '0');
	for (int i = len1 - 1; i >= 0; i--){
		for (int j = len2 - 1; j >= 0; j--){
			int t = (res[i + j + 1] - '0') + (num1[i] - '0')*(num2[j] - '0');
			res[i + j + 1] = t % 10 + '0';
			res[i + j] += t / 10;
		}
	}
	for (int i = 0; i<len1 + len2; i++){
		if (res[i] != '0') return res.substr(i);
	}
	return "0";
}

int main(){
	string s1, s2;
	cin >> s1 >> s2;

	cout << "相加:" << addstr(s1,s2) << endl;
	cout << "相乘:" << multiply(s1, s2) << endl;

	return 0;
}

在这里插入图片描述

三、编辑距离问题

题目地址

编辑距离，又称Levenshtein距离，是指两个子串之间，由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。请尝试写出一个算法来计算两个字符串的编辑距离。

1、当min(i,j)=0时，f(i,j)=max(i,j)，一个字符串的长度为0，编辑距离是另一个字符串的长度
2、当a[i]=b[j]时，f(i,j)=f(i−1,j−1)，比如xxcz和xyz的距离=xxc和xy的距离
3、否则，lev(i,j)为如下三项的最小值：
f(i−1,j)+1(在a中删除ai);
f(i,j−1)+1(在a中插入bj);
f(i−1,j−1)+1(在a中把ai替换bj)，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;

//编辑距离
int EditDistance(string s1, string s2) {
	int m = s1.size(), n = s2.size();
	vector<vector<int>> arr(m + 1, vector<int>(n + 1));
	for (int i = 0; i <= m; i++){
		for (int j = 0; j <= n; j++){
			if (i == 0 || j == 0){
				arr[i][j] = max(i, j);
			}
			else if(s1[i-1] == s2[j-1]){ //注意
				arr[i][j] = arr[i - 1][j - 1];
			}
			else{
				arr[i][j] = min(arr[i - 1][j] + 1, min(arr[i][j-1] + 1, arr[i - 1][j - 1] + 1));
			}
		}
	}
	return arr[m][n];
}

int main(){
	string s1, s2;
	cin >> s1 >> s2;

	cout << EditDistance(s1, s2) << endl;

	return 0;
}

时间复杂度O（nm)， 空间复杂度O（nm）

四、kmp算法

题目地址

给定两个字符串str和match，长度分别为N和M。实现一个算法，如果字符串str中含有子串match，则返回match在str中的开始位置，不含有则返回-1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
#include <iostream>
#include <vector>
#include <string>
using namespace std;

// 暴力匹配算法
int ViolentMatch(string s, string p) {
	int i = 0, j = 0, slen = s.size(), plen = p.size();
	while (i < slen && j < plen)
	{
		if (s[i] == p[j]){
			i++;
			j++;
		}
		else{
			i = i - j + 1;
			j = 0;
		}
	}
	
	if (j == plen) return i - j;
	else return -1;
}

// KMP算法
int KMP(string s, string p, vector<int>next) {
	int i = 0, j = 0, slen = s.size(), plen = p.size();
	while (i < slen && j < plen)
	{
		if (j == -1 || s[i] == p[j]){
			i++;
			j++;
		}
		else{
			j = next[j];
		}
	}

	if (j == plen) return i - j;
	else return -1;
}

// MultiKMP算法
vector<int> MultiKMP(string s, string p, vector<int>next) {
	vector<int> res;
	int i = 0, j = 0, slen = s.size(), plen = p.size();
	while (i < slen)
	{
		if (j == -1 || s[i] == p[j]){
			i++;
			j++;
		}
		else{
			j = next[j];
		}
		if (j == plen){
			res.push_back(i - j);
			j = 0;
		}
	}
	return res;
}

// MultiKMP2算法
vector<int> MultiKMP2(string s, string p, vector<int>next) {
	vector<int> res;
	int i = 0, j = 0, slen = s.size(), plen = p.size();
	while (i < slen)
	{
		if (j == -1 || s[i] == p[j]){
			i++;
			j++;
		}
		else{
			j = next[j];
		}
		if (j == plen){
			res.push_back(i - j);
			i = i - j + 1;
			j = 0;
		}
	}
	return res;
}

vector<int> GetNext(string p)
{
	vector<int> next(p.size());
	next[0] = -1;
	int k = -1, j = 0;
	while (j < p.size() - 1)
	{
		//p[k]表示前缀，p[j]表示后缀  
		if (k == -1 || p[j] == p[k]){
			++k;
			++j;
			if (p[j] != p[k]) next[j] = k;
			else next[j] = next[k];
		}
		else{
			k = next[k];
		}
	}
	return next;
}

void printvec(vector<int> vec) {
	if (!vec.empty()){
		for (int i = 0; i < vec.size(); i++){
			cout << vec[i] << ' ';
		}
		cout << endl;
	}
	else{
		cout << -1 << endl;
	}
}

int main(){
	string s1, s2;
	cin >> s1 >> s2;

	vector<int> next = GetNext(s2);

	// 暴力匹配第一次出现位置
	cout << ViolentMatch(s1, s2) << endl;

	// KMP匹配第一次出现位置
	cout << KMP(s1, s2, next) << endl;

	// KMP匹配无重复所有出现位置
	vector<int> res = MultiKMP(s1, s2, next);
	printvec(res);

	// KMP匹配可重复所有出现位置
	vector<int> res2 = MultiKMP2(s1, s2, next);
	printvec(res2);

	return 0;
}

在这里插入图片描述
算法详解 时间复杂度为O(m + n)
扩展：BM算法、Sunday算法。

五、dijkstra算法

迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。它解决的是带权重的有向图上单源最短路径问题。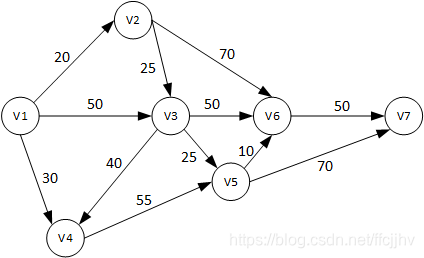
在这里插入图片描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#include <iostream>
#include <string>

using namespace std;

const int maxn = 100; // 最大顶点数
int map[maxn][maxn]; // 邻接矩阵存图
int dis[maxn]; // dist[i]表示距离源点的最短距离
int vis[maxn];  // vis[i] = 1表示已加入集合S
int path[maxn]; // 记录路径
int n, m, r;

void dijk(int s) // 求顶点s到其他顶点的最短路径
{
	//初始化
	memset(path, -1, sizeof(path));
	/*INF使用0x3f3f3f3f的好处：
	* 1：满足无穷大加一个有穷的数依然是无穷大（在DijKstra算法松弛操作中避免了溢出而出现负数）
	* 2：满足无穷大加无穷大依然是无穷大（两个0x3f3f3f3f相加并未溢出）
	* 3：初始化时，由于每一个字节为0x3f，所以只需要memset（buf，0x3f,sizeof(buf)）即可
	*/
	memset(dis, 0x3f, sizeof(dis)); //初始化为无穷大
	memset(vis, 0, sizeof(vis));
	dis[s] = 0; //自身到自身的距离为0
	while (1)
	{
		int k = 0;
		for (int j = 1; j <= n; j++)
		{
			if (!vis[j] && dis[j]<dis[k])//找未收录顶点中dis值最小的
				k = j; //这里第一次找到的是起点
		}
		if (!k) return; //没有未收录的点，则返回
		vis[k] = 1;
		//松弛操作
		for (int j = 1; j <= n; j++)
		{
			//第一次循环只有起点的邻接点距离被更新，每次都更新新找到的点的邻接点
			if (dis[j]>dis[k] + map[k][j])
			{
				dis[j] = dis[k] + map[k][j];
				path[j] = k;//路径被改变，重新记录前驱，最短路是由最短路+某一条固定路组成，所以前驱是有效的
			}
		}
	}
}

void printPath(int x)
{
	if (x == -1) 
		return;
	//递归
	printPath(path[x]);
	if (x == r) 
		cout << x;
	else 
		cout << " -> " << x;
}


/*问题描述：
* 输入n,m和r，代表n个节点，m条边，出发点r，然后是m行输入，每行有x,y,z，代表x到y的路距离为z。
* 问题：从r出发到各点的最短路径。
*/

int main()
{
	cin >> n >> m >> r;

	memset(map, 0x3f, sizeof(map));

	int x, y, z;
	for (int i = 1; i <= m; i++)
	{
		cin >> x >> y >> z;
		if (map[x][y] > z){ // 防止1->1的环
			map[x][y] = z;
			//map[y][x] = z; // 无向图
		}
	}

	dijk(r);

	for (int i = 1; i <= n; i++){
		printPath(i);
		cout<< " "<< dis[i];
		cout<< endl;
	}

	return 0;
}

在这里插入图片描述
算法详解 算法详解 时间复杂度为O( n^2)

六、0/1背包问题

在这里插入图片描述
0/1背包问题:满足总重量<=背包重量限制，使价值最大。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int ZeroOnePack(int m, int s, vector<int> weight, vector<int> value) {
	// F[i ][ v] 表示  前i件物品恰放入一个容量恰为v的背包可以获得的最大价值
	vector<vector<int> > F(m + 1, vector<int>(s + 1));
	for (int i = 0; i <= s; i++) {
		F[0][i] = 0; //如果要求恰好装满背包，除了F[0]为0，其余F[1 .. s]均设为-INF
	}
	for (int i = 1; i <= m; i++){
		for (int j = 0; j <= s; j++){
			if (j >= weight[i - 1])
				F[i][j] = max(F[i - 1][j], F[i - 1][j - weight[i - 1]] + value[i - 1]);
			else
				F[i][j] = F[i - 1][j];
		}
	}

	//打印哪几样物品能够获得最大价值
	vector<bool> isAdd(m,false);
	int j = s;
	for (int i = m; i >= 1; i--){
		if (F[i][j] != F[i - 1][j]){
			isAdd[i - 1] = true;
			j = j - weight[i - 1];
		}
	}
	for (int i = 0; i < m; i++){
		cout << isAdd[i] << " ";
	}
	cout << endl;

	return F[m][s];
}

int main() {
	int m, s; // 物品种类m，背包总空间t，求最大价值
	cin >> m >> s;

	vector<int> weight;
	vector<int> value;
	for (int i = 0; i < m; i++){
		int t1, t2;
		cin >> t1 >> t2;
		weight.push_back(t1);
		value.push_back(t2);
	}

	int res = ZeroOnePack(m, s, weight, value);
	cout << res << endl;

	return 0;
}

在这里插入图片描述
算法详解

0%